🧶
[프로그래머스] 섬 연결하기
January 25, 2023
1. 문제
프로그래머스
2. 핵심 아이디어
그리디 크루스칼
3. 코드
import Foundation
var parentNumber: [Int] = []
func solution(_ n:Int, _ costs:[[Int]]) -> Int {
parentNumber = (0..<n).map{$0}
let costs = costs.sorted { lhs, rhs in
return lhs[2] <= rhs[2]
}
var sum = 0
for bridge in costs {
if !isCycle(left: bridge[0], right: bridge[1]) {
changeParent(oldParent: parentNumber[bridge[1]], newParent: parentNumber[bridge[0]])
sum += bridge[2]
}
}
return sum
}
func isCycle(left:Int, right:Int) -> Bool {
return parentNumber[left] == parentNumber[right]
}
func changeParent(oldParent:Int,newParent:Int) {
parentNumber.indices.filter {parentNumber[$0] == oldParent}.forEach{parentNumber[$0] = newParent}
}4. 풀이 과정
최단 경로를 우선 탐색하면 되지 않을까?
1. 노드 하나 선택 -> DFS 로 연결된 방문하지 않은 다른 2. 노드 까지의 방문 거리를 업데이트 (최소 거리)
3. 가장 짧은 거리의 노드로 이동.
4. 반복
-> 이게 다익스트라인가?결론은 다익스트라 같은 알고리즘을 쓰면 될 것 같은데? 라는 생각을 가지게 되었고, 찾아봤는데..
크루스칼 이라는 비슷하면서 많이 다른 알고리즘이 이 문제 풀이에 더 맞다는 것을 알게되었다.
크루스칼 알고리즘 이란?
크루스칼 알고리즘은 최소 신장 트리를 찾기위해 고안된 알고리즘이다.
이 알고리즘에서는 오름차순 정렬 과 Union & Find 가 활용된다.
최소 신장 트리
우선 신장 트리 (spanning-tree) 란
1. 모든 정점을 포함한다.
2. 정점 간 서로 연결되고 싸이클이 존재하지 않는다.이 두가지 조건을 만족하는 그래프이다.
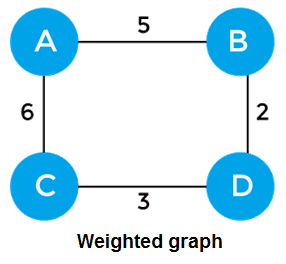
이와 같이 모든 정점이 연결되어 있고 가중치가 있는 그래프가 있다면
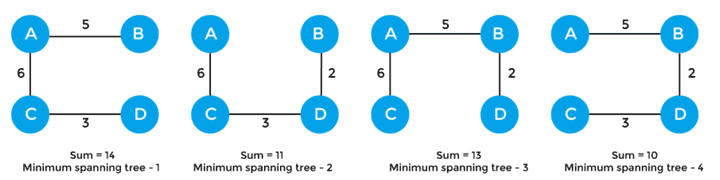
이렇게 4가지의 신장 트리가 만들어질 수 있다.
이중에 최소 신장 트리는 간선의 가중치의 합이 가장 적은 4번째 신장 트리이다.
구현
크루스칼 알고리즘에서는 먼저 가중치의 오름차순으로 정렬한 후, 정렬된 순서대로 간선을 추가한다.
간선을 추가하는 과정에서 Union & Find가 활용되는데, 서로 중복되지 않는 집합을 표현하기 위해 사용된다.
구체적인 동작 과정은 이곳을 참고하면된다.
구현의 핵심 아이디어는 요약하자면 최소 가중치 순차 추가, Union & Find 로 싸이클 여부 확인이다.
다익스트라와 크루스칼 알고리즘의 차이점은 조건이라고 생각한다.
다익스트라는 특정한 두개의 정점의 최소 거리를 찾을 때 사용하고
크루스칼은 모든 정점이 연결되기 위한 (사이클 없이) 최소 비용을 찾을 때 사용하면 좋다.
참고
크루스칼의 구현과 설명을 이곳에서 참조하였다.